Case Study: Geography
Main Content
Geography, an important factor in data analysis
Introduction
This study has been created to show how the interpretation of a single dataset can change when considering data presented at different geographies.
The study will firstly discuss the layers of statistical geographies that have been created by Neighbourhood Statistics.
Secondly it will show how the areas which show low percentage of full-time employees at one layer of geography may differ to those areas highlighted when smaller geographies are investigated.
This case study is also available as a pdf document (345Kb).
Section 1: Data
This study will use the 2001 Census 'Economic Activity' (table KS09a) which is stored in the '2001 Census', 'Work Deprivation' and 'Indicators' domains of the Neighbourhood Statistics website.
The 2001 Census Economic Activity dataset has a number of variables, including counts and percentages of all people aged between 16-74 and their economic activity. The study will investigate the percentage of full-time employees.
The technique
The study will discuss the layers of the Neighbourhood Statistics geography hierarchy and how viewing data at different geographical layers can affect the interpretation of the data.
Understanding the geographies
There are a multitude of geographies that can be used for analysis. To aid analysis, Neighbourhood Statistics has generated a statistical geography hierarchy.
This hierarchy has been developed with the aim of improving the usefulness of small area statistics by creating a more stable, reliable set of building blocks.
These building blocks were designed using the 2001 Census. The advantage of this hierarchy is that data are available on smaller, more comparable geographies.
There are four geographies that will be discussed in this study. The bottom three are part of the statistical hierarchy:
- Local Authority - LA,
- Middle Layer Super Output Area - MSOA,
- Lower Layer Super Output Area - LSOA,
- Output Area - OA.
Local authority - LA
Local authority is a generic term for any level of local government in the UK. LAs include non-metropolitan districts, metropolitan districts, unitary authorities and London boroughs (in England); Welsh unitary authorities; Scottish council areas; and Northern Irish district council areas.
Middle Layer Super Output Area - (MSOA)
These areas have a minimum population of 5,000, with an overall mean of 7,200. They were built from groups of Lower Layer Super Output Areas and constrained by the local authority boundaries of 2003. There are around 7,000 MSOAs in England and Wales.
Lower Layer Super Output Area - (LSOA)
These have a minimum population of 1,000, with an overall mean of 1,500. They are built from groups of Output Areas. There are around 34,000 LSOAs in England and Wales.
Output Area - (OA)
In England and Wales OAs were designed from the 2001 Census. Postcodes were grouped into OAs according to a set of design criteria. OAs have a minimum population size of 100 with an overall mean of 300. There are around 175,000 OAs in England and Wales.
As a result of the 2011 Census changes were identified which resulted in the creation of the 2011 Statistical Geography Hierarchy. This new hierarchy superseded the 2001 Statistical Geography hierarchy which was created following the 2001 Census. Full details of the changes are provided by ONS Geography.
Data available for statistical geographies
Neighbourhood Statistics is constantly striving to increase the amount of data available. As time goes by it is expected that more and more datasets will become available. However, there is already a vast amount of data available for this statistical hierarchy aiming to help understanding of issues of deprivation in small areas.
Understanding the hierarchy
Figure 1: Statistical hierarchy.

The future of Neighbourhood Statistics Geography
The MSOA, LSOA and OA geographies are the building blocks upon which the National Statistics 'Geography Policy' is built. Follow this link for more information on the National Statistics Geography Policy.
Section 2: Mapping 'Economic Activity - Full-time Employees'
We can map the areas that are present in the lowest 10 per cent of the data i.e. as there were 354 local authorities in England at the time the data in the example was published, we will consider the 35 (354/10) that have the lowest percentage of full-time resident employees in 2001.
Map 1: The 35 local authorities that have the lowest percentage of full-time resident employees, based on data from the 2001 Census, across England.

The map shows the geographical spread of these local authorities across England. It highlights a cluster of local authorities in the South West and East of England that have a low percentage of full-time employees.
What it does not show is how the percentage of full-time employees is distributed through each local authority area.
Rather than investigating the percentage of full-time employees across all England, we will instead consider a single Government Office Region (GOR).
For the rest of the study we will investigate the percentage of full-time employees in the East of England GOR. However, these steps of analysis can be repeated for any region or area.
Middle Layer Super Output Areas
We can continue our investigation into the percentage of full-time employees by repeating the same process of highlighting the MSOAs that fall within the lowest 10 per cent of full-time employees in the East of England.
Map 2: The MSOAs in the lowest 10 per cent for full-time employees across England but geographically located in the East of England GOR

It is difficult to tell from Map 2 the differences between the MSOA and the local authority areas. However, if we overlay the local authority areas with the MSOA areas we can see the effect.
Map 3: Comparison between local authority areas and MSOAs with the lowest 10 per cent of full-time employees across England but geographically located in the East of England
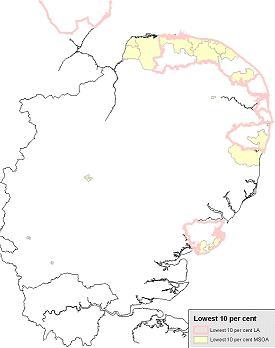
shows that those areas present in the lowest 10 per cent of full-time employees using MSOA geography, are different from those that are within the lowest 10 per cent for local authority areas. It is easy to see the differences when investigating at this lower geographical layer.
The advantage of using the MSOA geography is that we are able to highlight much smaller areas for investigation. This potentially makes targeting of resources more effective. However, there are currently only a few datasets available at this geography.
Lower Layer Super Output Areas
We can continue down to the Lower Layer Super Output Area geography to discover the affects of analysing data at an even smaller geography.
Map 4: The LSOAs in the lowest 10 per cent for full-time employees across England but geographically located in the East of England GOR
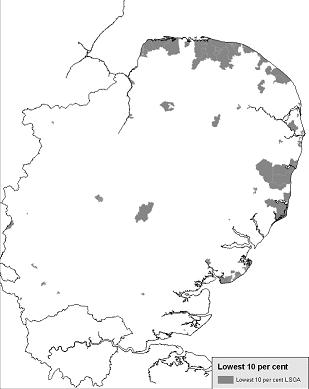
Again we have found areas that have not been captured by the two higher layers of geography. This shows the advantage of using an even lower layer of geography. It will show areas that are masked by the averaging effect at a higher layer of geography.
To help understand where the differences between the three geographical layers are, we can overlay the areas that are within the lowest 10 per cent for local authority areas, MSOAs and LSOAs.
Map 5: Comparison between local authority areas, MSOAs and LSOAs with the lowest 10 per cent of full-time employees across England but geographically located in North Norfolk local authority

Map 5 shows the local authority of North Norfolk in the East of England. By zooming into a local authority in this way, we can see the distinct areas that have low numbers of full-time employees. This local authority has been chosen as we are already aware that it is one of the 35 local authorities with the lowest percentage of full-time employees. However, from the map it can be seen that the pattern is different depending on which geography you look at. We are able to see that some areas overlap between the geographies and some are distinct from each other.
Can we investigate the lowest layer of geography - the Output Areas?
Output Areas
When investigating the data for this analysis we found that data at the Output Area layer are affected by the risk of disclosing confidential information. We know this to be the case as the data on the Neighbourhood Statistics website have been suppressed at this geography. This means the LSOA is the lowest geography layer that this particular data can be analysed on.
In conducting this analysis we have highlighted two things:
- we have been able to drill down within already highlighted areas to find where the most affected areas are;
- we have found areas that are only highlighted when the lower geographies are investigated.
What can we say about the analysis?
What can we say about the analysis? By using the one variable, 'Percentage of Full-time Employees' from the 2001 Census, we have considered how the message presented by the data differs depending on the geography used. But what does it actually show and what does it mean for our analysis?
In doing this analysis we have shown how easy it is for messages that are visible at smaller geographies to be hidden when considering higher layers of geography. This obviously has a big impact on the interpretation of the data. Choosing the correct geography is paramount to highlighting the real issues.
However, it is not simply a case of choosing the lowest layer of geography. We have seen that the confidentiality of the data becomes a greater issue when looking at small geographies. This is a particular problem if the issue that you are dealing with has a small number of events. It may even have such an impact that it may not be possible to analyse the data on small geographies at all.
Even when this is not the case and data are available at this small geography there are some key points to consider. Firstly the data that are supplied by Neighbourhood Statistics may have been subjected to measures that help to maintain confidentiality. Although necessary to ensure confidentiality it is easy to imagine the issues this raises for your analysis, especially if the data values have been rounded.
Another thing to consider when using Output Areas is the sheer number you will have to investigate. We know that there are around 175,000 present in England and Wales. This in itself will add a unique set of issues when analysing at this geographical level.
Summary
This analysis has hopefully provided you with a brief insight into the different geographies for which Neighbourhood Statistics data are available.
The study has shown how each of the SOA hierarchy relate to each other , each being built from the one below and constrained by geography layers above.
Also, by looking at the percentage of full-time employees from the Census, we have investigated how presenting data at different geographical layers can affect the interpretation of data. We have shown how the messages within the data at the higher layers of geography differ to those seen at the lower geographies.
The study has hopefully highlighted the need to be aware of what happens to data when lower and lower geographies are considered. The data we have used have shown how the messages change just because a different geography is investigated. It is important to understand that changes happen due to the geographical changes and would happen to a lesser or greater extent whatever topic you are investigating. The point is, unless you investigate at these lower geographies then deprived areas could remain hidden and the extent of problems be unknown.
Choosing the right geography is a key element of creating good meaningful analysis. This is done by achieving a balance of three elements that have been raised in this study.
- The level of detail a geography will give
- What data are available and how they are affected by confidentiality issues
- The amount of data that are present for your geography of interest and how easy it is to actually analyse the amount of data needed.
This study has only covered the statistical hierarchy that is present on Neighbourhood Statistics. There are also data currently available for a range of geographical boundaries. Follow this link for more information on Neighbourhood Statistics geography.
